1. 설명
상관분석은 서로 짝지어진 두 변수 사이의 관계의 강도를 [-1,1] 의 값을 갖는 상관계수로 나타내는 분석방법입니다. 0이면 관계 없음, 1에 가까울 수록 비례관계, -1에 가까울 수록 반비례관계입니다. 상관계수를 판단하는 일반적 기준은 아래와 같습니다.
0.0~0.2 : very weak correlation (or negligible)
0.2~0.4 : weak correlation
0.4~0.6 : moderate correlation
0.6~0.8 : strong correlation
0.8~1.0 : very strong correlation
절대적 기준은 아닙니다. 예를들어 '암과의 상관관계' 라면 낮은 상관계수도 유의미하게 해석될 수 있습니다.
상관계수에 대한 가설검정도 수행합니다.
귀무가설 : 상관계수=0
대립가설 : 상관계수≠0
따라서 R에서 상관분석을 수행하면 두가지 결과가 출력됩니다.
출력 결과 : 상관계수, p-value
상관분석에는 세가지 방법이 있습니다.
Pearson : 모수적 방법
Kendall : 비모수적 방법, 순위자료로 전환 후 피어슨상관계수 구함
Spaerman : 비모수적 방법, 부합인 쌍의 수가 P, 비부합인 쌍의 수가 Q일 때 P-Q/P+Q 로 정의됨
피어슨 상관분석을 공부하는 강의이므로, 피어슨상관분석만 설명드리겠습니다. 피어슨 상관계수의 정의는 아래와 같습니다.
$$\rho _{xy}=\frac{cov(X,Y)}{\sigma _{x}\sigma _{y}}$$
표본의 상관계수는 r이라고 부릅니다. 크기 n인 표본의 경우 아래와 같이 구합니다.
$$r_{xy}=\frac{\sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )\left ( y_{i}-\bar{y} \right )}
{\sqrt{\sum_{i=1}^{n}\left ( x_{i}-\bar{x} \right )^{2}}\sqrt{\sum_{i=1}^{n}\left ( y_{i}-\bar{y} \right )^{2}}}$$
두 변수의 공분산을 각 변수의 표준편차로 나눈 것입니다. 표준편차로 나눈것은 -1~1 사이로 normalize 하기 위함이고, 공분산의 의미가 핵심입니다. 공분산은 한 변수의 값이 커질 때 다른 변수의 값도 커지는 경향이 있으면 양수값, 한 값이 커질 때 다른 값이 작아지는 경향을 보이면 음수 값을 갖습니다.
두 변수가 비례하는 경향 -> 공분산 양수
두 변수가 반비례하는 경향 -> 공분산 음수
하지만 공분산 값 자체로 상관관계의 정도를 나타내기는 어렵습니다. 단위가 다르면 천차만별로 달라지기 때문입니다. 따라서 각 변수의 표준편차로 나누어 -1~1사이로 표준화시킨 값을 사용합니다. 이 값이 피어슨상관계수입니다.
2. 대상
서로 짝지어진(paired) 데이터
ex) 성인 30명의 키와 몸무게
3. R 함수와 옵션
cor.test 함수를 사용합니다.
cor.test(x, y, alternative = c("two.sided", "less", "greater"), method = c("pearson", "kendall", "spearman"), exact = NULL, conf.level = 0.95, continuity = FALSE, ...)
아래는 옵션 설명입니다. 피어슨 검정을 할 때는 alternative 이외의 옵션은 신경 안써도 됩니다. exact나 continuity 는 피어슨과 무관한 옵션입니다.
alternative : 단측, 양측 여부 결정. 단측일 경우 상관관계가 0보다 큰지, 작은지에 관심. 양측일 경우 상관관계가 0인지 아닌지에 관심
4. 피어슨 상관분석 예시
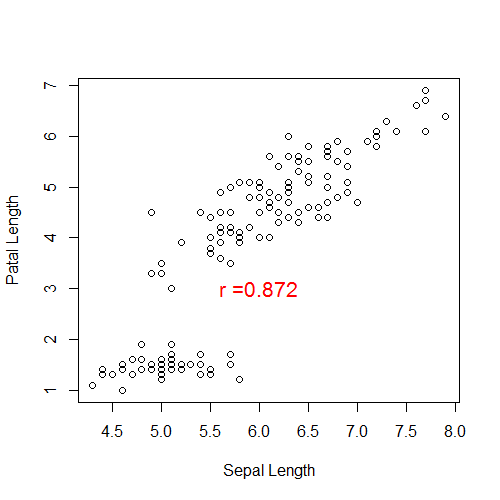
내장데이터인 iris 를 이용하였습니다. Sepal.Length 와 Petal.Length 로 상관분석을 수행하였습니다.
> cor.test(iris$Sepal.Length,iris$Petal.Length)
Pearson's product-moment correlation
data: iris$Sepal.Length and iris$Petal.Length
t = 21.646, df = 148, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8270363 0.9055080
sample estimates:
cor
0.8717538
상관계수는 0.87이 나왔고, p값은 <0.001 입니다. 상관계수는 0이 아니고, 아주 강한 상관관계입니다.
5. 시각화
그래프를 그려봅시다. 아래 코드를 사용합니다.
crrltn=cor.test(iris$Sepal.Length,iris$Petal.Length)
plot(iris$Sepal.Length,iris$Petal.Length,ann=FALSE)
title(xlab="Sepal Length",ylab="Patal Length")
text(6.0,3,paste0("r =",round(crrltn$estimate,3)),cex=1.3,col="red")
'R 주제 > R 기초 및 통계 강의' 카테고리의 다른 글
| [R강의] 108. 표준정규분포표 만들기 (0) | 2021.03.22 |
|---|---|
| [R강의] 107. 히스토그램에서 density는 상대도수가 아닙니다. (0) | 2021.01.07 |
| [R강의] 105. attr 이 무엇인가요? (0) | 2020.10.03 |
| [R강의] 104. 데이터프레임의 구조확인 str함수 vs glimpse 함수 (0) | 2020.10.02 |
| [R 강의] 103. 정말 유용한 %>% 연산자 (0) | 2020.10.02 |


댓글